CFD for Moving Boundaries and Interfaces

Simulating Flows Around Moving Boundaries and Interfaces (MBI) in OpenFOAM

OpenFOAM is a powerful open-source tool for computational fluid dynamics (CFD) that offers extensive capabilities for simulating fluid flows in complex geometries. One of OpenFOAM's strengths is its ability to model and simulate flows around moving boundaries and interfaces (MBI), which is essential for a wide range of engineering applications, from rotating machinery to vehicles and biological flows. This tutorial provides an introduction to the various classes of motions that can be simulated in OpenFOAM, including prescribed motion, rigid body motion, sliding meshes, and multiple reference frames. Understanding these capabilities will enable you to leverage OpenFOAM's full potential for your fluid dynamics simulations.

Prescribed Motion

Prescribed motion refers to scenarios where the movement of the boundary or interface is known a priori and is explicitly defined within the simulation setup. This could involve simple translational or rotational motions or more complex, time-dependent paths. In OpenFOAM, prescribed motions are often implemented using boundary conditions or mesh motion solvers that enforce the specified motion on the fluid domain's boundaries. This approach is ideal for simulating scenarios like the oscillating motion of an airfoil or the predetermined path of a moving object through a fluid.

Rigid Body Motion

Rigid body motion involves simulating the movement of solid objects within the fluid domain, where the object's deformation is negligible. OpenFOAM uses the sixDoFRigidBodyMotion solver to model the dynamics of rigid bodies under the influence of fluid forces, enabling the simulation of phenomena such as a floating buoy's response to wave action or a vehicle's aerodynamic behavior. The solver calculates the object's position and orientation over time based on the forces and moments acting on it, taking into account the mass properties and external constraints.

Sliding Meshes

Sliding meshes are used to simulate the interface between two or more moving parts of the domain, where at least one part is in motion relative to the others. This technique allows for the accurate simulation of relative motion without the need for remeshing, making it suitable for applications like rotating machinery (e.g., turbines, pumps, and compressors) where components move independently. OpenFOAM implements sliding meshes through the dynamic mesh library, allowing the mesh to deform and the interfaces between different regions to slide over each other, providing a realistic representation of the flow dynamics in these systems.

Sliding meshes in OpenFOAM are a crucial tool for accurately simulating the dynamic interaction between moving parts within a fluid domain. Unlike the MRF approach, which simplifies the domain into stationary and rotating regions, sliding meshes allow for a more detailed and dynamic representation of the relative motion between different parts of the machinery. This method is particularly valuable in scenarios where components move independently and possibly with non-uniform velocities, necessitating a dynamic adaptation of the mesh to accurately capture the interface dynamics.

Key Characteristics of Sliding Meshes

Dynamic Mesh Adaptation: The mesh near the interface between moving parts dynamically adjusts to accommodate the relative motion, ensuring that the integrity of the mesh is maintained, and the flow is resolved accurately at all times.
Accurate Flow Representation: By allowing the mesh to slide and adapt, this method provides a more realistic simulation of the fluid dynamics at the interfaces, capturing complex flow patterns such as shear layers, vortices, and flow separation.
Application Versatility: Ideal for simulating rotating machinery with complex motion patterns, including turbines with pitch-adjustable blades, gear pumps, and machinery where components have translational and rotational movements.

Implementation Considerations

Implementing sliding meshes in OpenFOAM involves several critical steps to ensure accurate and stable simulations:

Mesh Configuration: The domain is divided into separate regions (or zones) that correspond to the different moving parts and the stationary part of the domain. Each zone has its mesh, which can slide relative to the others.
Boundary Conditions: Appropriate boundary conditions are applied at the interfaces between sliding meshes to ensure continuity of flow variables (velocity, pressure, etc.) across the moving boundaries.
Solver Configuration: Solvers that support dynamic mesh handling are used, configured to update the mesh continuously as the simulation progresses, based on the predefined motion of the domain parts.

Mathematical Formulation

The mathematical formulation for sliding mesh simulations modifies the Navier-Stokes equations to accommodate the moving mesh. The primary adjustment is in the advection term, which now accounts for the mesh velocity ($\mathbf{u}_\mathrm{mesh}$):

$$ \frac{\partial (\rho \mathbf{u})}{\partial t} + \nabla \cdot (\rho (\mathbf{u} - \mathbf{u}_\mathrm{mesh}) \mathbf{u}) = -\nabla p + \nabla \cdot \mathbf{\tau} + \rho \mathbf{g} $$

Here, the relative velocity $(\mathbf{u} - \mathbf{u}_\mathrm{mesh})$ accounts for the motion of the mesh itself, ensuring that the flow is correctly simulated relative to the moving parts.

Real-World Applications

Turbines with Adjustable Blades: Sliding meshes can simulate the flow dynamics as the blades of a wind turbine adjust to changing wind conditions, capturing the effects of blade movement on performance.
Gear Pumps: In pumps where gears rotate independently and interact with the fluid, sliding meshes accurately model the fluid flow between the teeth and around the gears.
Variable Geometry Turbines: For turbines where the stator blades can move to optimize efficiency under different operating conditions, sliding meshes offer a way to simulate the complex interactions between the blades and the flow.

In summary, sliding meshes provide a flexible and accurate method for simulating the dynamic interactions between moving parts in fluid domains, essential for designing and optimizing performance in a wide range of mechanical systems.

Multiple Reference Frames (MRF)

The Multiple Reference Frames (MRF) approach is used to simplify the simulation of rotating machinery by dividing the domain into stationary and rotating regions. In the rotating region, the flow is solved relative to a rotating reference frame, avoiding the need to simulate the actual motion of the mesh. This method is particularly effective for steady-state simulations of devices like fans, mixers, and marine propellers, where the rotation can be assumed to be constant. MRF simplifies the computational model and reduces the computational cost while still capturing the essential features of the flow around rotating parts.

The Multiple Reference Frames (MRF) method in OpenFOAM is a powerful approach to simulate the flow around rotating parts in machinery without the computational expense of moving the mesh. When adopting the MRF approach, it is important to consider the effects of fictitious forces that arise due to the non-inertial (rotating) reference frame. These include the Coriolis force and the centrifugal force, which significantly affect the flow characteristics within the rotating region.

Fictitious Forces in MRF

Centrifugal Force: This is a radial outward force observed in the rotating frame of reference. It results from the rotation and acts perpendicular to the axis of rotation. In a rotating machinery simulation, this force influences the radial distribution of pressure and velocity within the flow field.
Coriolis Force: This force acts on fluid particles moving within the rotating reference frame and is orthogonal to the particle velocity and the axis of rotation. The Coriolis force affects the flow path of the fluid, causing it to curve. Its impact is particularly noticeable in applications involving high rotational speeds or large radial velocities.

Navier-Stokes Equations for Non-Inertial Reference Frames

To account for these forces, the Navier-Stokes equations are modified for non-inertial reference frames. In a rotating reference frame, the conservation of momentum equation (a form of the Navier-Stokes equations) can be expressed as:

$$ \frac{\partial (\rho \mathbf{u})}{\partial t} + \nabla \cdot (\rho \mathbf{u} \mathbf{u}) = -\nabla p + \nabla \cdot \mathbf{\tau} + \rho \mathbf{g} + \rho \mathbf{F}_{\mathrm{centrifugal}} + \rho \mathbf{F}_{\mathrm{Coriolis}} $$

where:

$\rho$ is the fluid density,
$\mathbf{u}$ is the velocity vector in the rotating frame,
$t$ is time,
$p$ is the pressure,
$\mathbf{\tau}$ is the viscous stress tensor,
$\mathbf{g}$ is the gravitational acceleration,
$\mathbf{F}_{\text{centrifugal}}$ is the centrifugal force per unit mass,
$\mathbf{F}_{\text{Coriolis}}$ is the Coriolis force per unit mass.

The expressions for the centrifugal and Coriolis forces per unit mass are given by:

$\mathbf{F}_{\text{centrifugal}} = -\omega \times (\omega \times \mathbf{r})$,
$\mathbf{F}_{\text{Coriolis}} = -2\omega \times \mathbf{u}$,

where:

$\omega$ is the angular velocity vector of the rotation,
$\mathbf{r}$ is the position vector from the axis of rotation to the point in the fluid,
$\times$ denotes the cross product.

These additional terms in the Navier-Stokes equations account for the influence of the rotating reference frame on the fluid flow. The centrifugal force contributes to the radial pressure gradient, while the Coriolis force affects the flow direction. Incorporating these effects into the simulation with the MRF method allows for accurate modeling of the fluid dynamics in rotating machinery, capturing the essential physics without the computational complexity of simulating the physical movement of the mesh.

Overset Mesh Method (not available in OpenFOAM v10)j

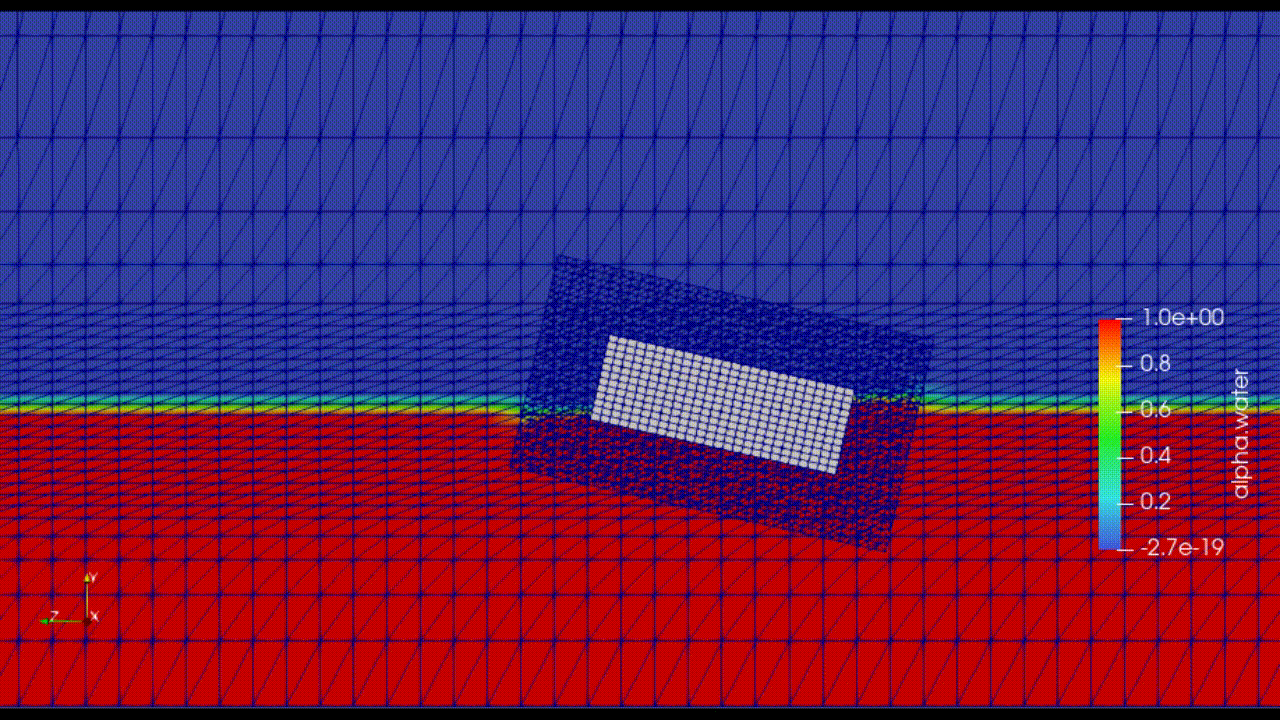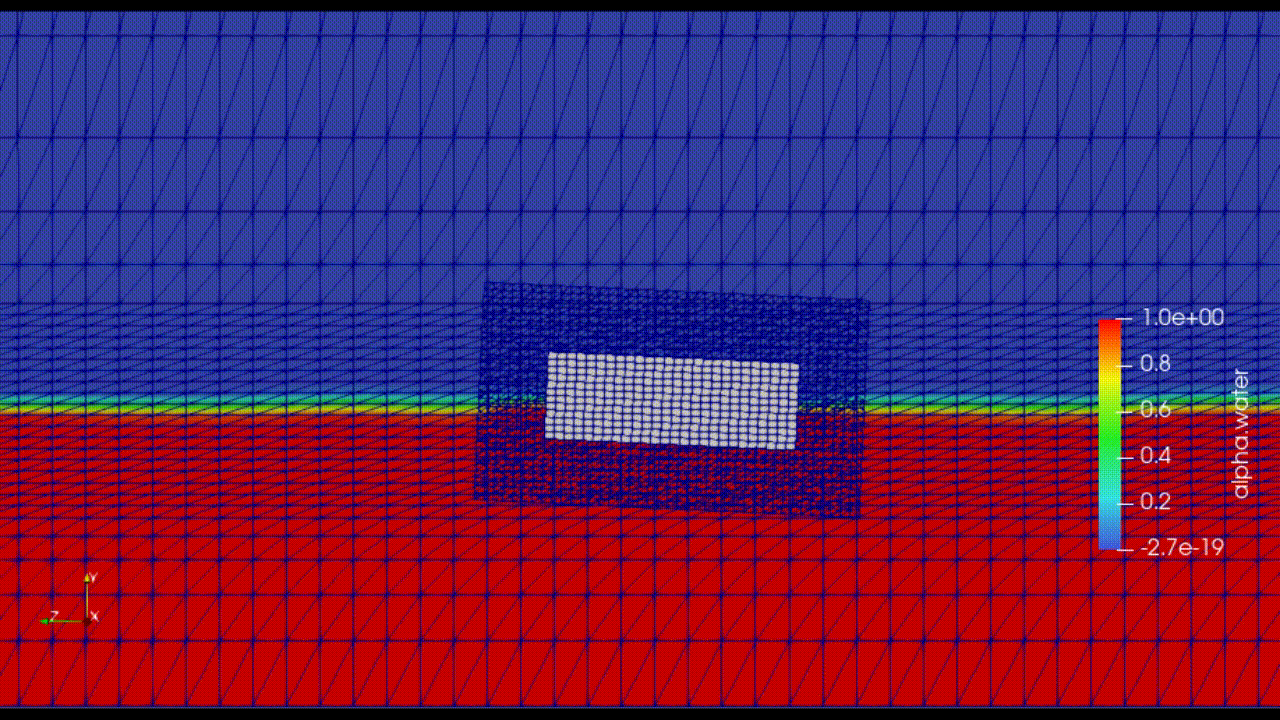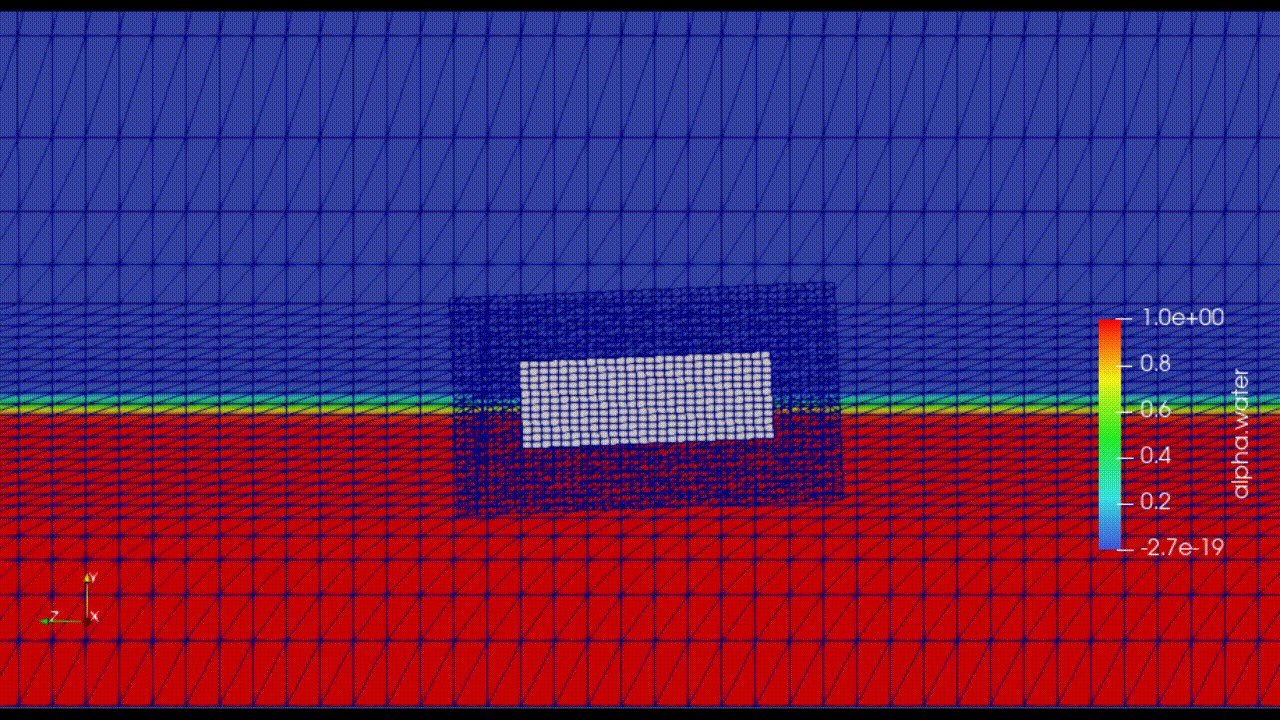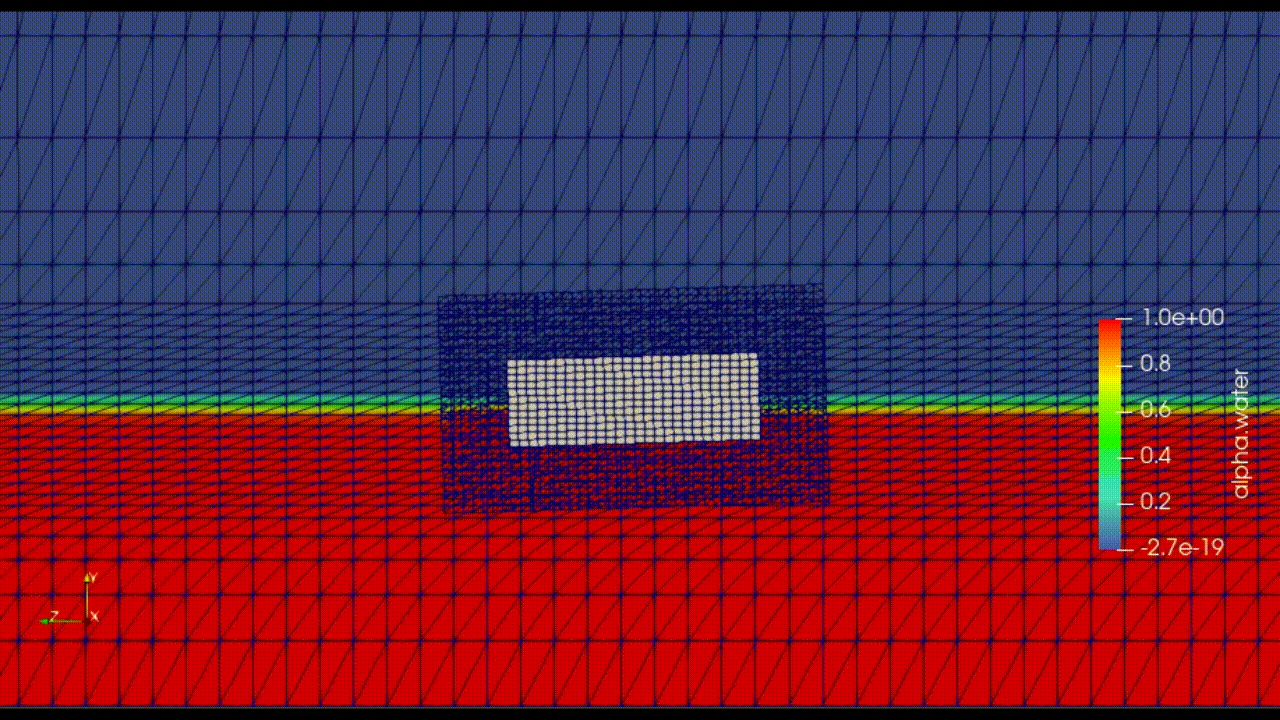
Image is taken from: https://www.services.aeroengineering.co.id/portfolio-item/floating-body-stability-modelling-using-overset-mesh/